This is part of my “artificial perception” project.
An image (16×16 pixels) is generated which consists of 8 horizontal and 8 vertical white bars with each being either shown or hidden by chance. This means there is a total of 2^16=65536 patterns possible. Additionally the generated image is degraded by adding 50% noise to make recognition harder (this ultimately increases the number of possible patterns to infinite).
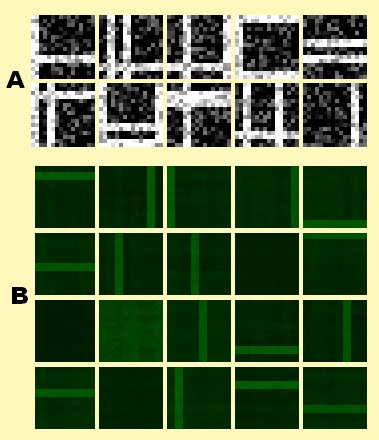
(A) shows a small subset of these input patterns.
Now these patterns are presented one-by-one (no batch processing) to a system consisting of 20 artificial neurons (amount is arbitrarily choosable) and each neuron updates its synapses by my new learning-rule.
The idea is that the system “learns to understand” the pattern-generating process and instead of trying to remember all possible patterns (65536 without noise and close to infinity for the noisy ones) which is completely unfeasable due to size constraints it extracts each bar seperately (even tho they are almost never shown in isolation, but always in combination with other bars). It does so as every pattern experienced so far can be reconstructed from these (2*8) separate bars.
(B) shows that 4 of the 20 neurons will remain unspecialized while the other 16 will specialize towards one of the 2*8 bars.
Also as you can see each neuron’s specialization in (B) is mainly free of noise (and therefore the whole percept) even tho a great amount of noise was inherent in each presented pattern.
This results in a 16-bit code which is the optimal solution to represent all patterns in a compact manner.
Computational complexity is O(N²) where N is the number of neurons. Memory complexity is just O(N).
Complexity is NOT dependent on the amount of patterns shown (or possible).
This should be one of the fastest online learning methods for this test without storing or processing previously experienced patterns.